10. Dielectrics

Dielectrics

Clear materials such as water, glass, and diamonds are dielectrics. When a light ray hits them, it splits into a reflected ray and a refracted (transmitted) ray. We’ll handle that by randomly choosing between reflection or refraction, and only generating one scattered ray per interaction.

Snell’s Law

The refraction is described by Snell’s law:

η⋅sin⁡θ=η′⋅sin⁡θ′\eta \cdot \sin\theta = \eta' \cdot \sin\theta'

Where θ\theta and θ′\theta' are the angles from the normal, and η\eta and η′\eta' (pronounced “eta” and “eta prime”) are the refractive indices (typically air = 1.0, glass = 1.3–1.7, diamond = 2.4). The geometry is:

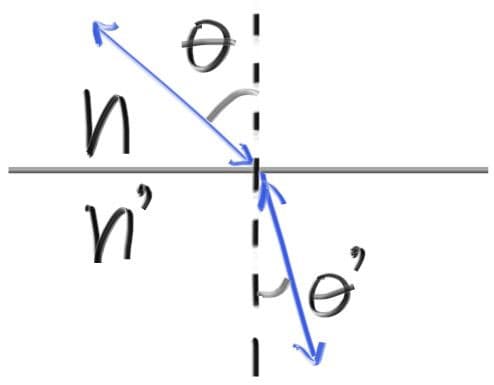
Ray refraction
Ray refraction

In order to determine the direction of the refracted ray, we have to solve for sin⁡θ′\sin\theta':

sin⁡θ′=ηη′⋅sin⁡θ\sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta

On the refracted side of the surface there is a refracted ray R′\mathbf{R'} and a normal n′\mathbf{n'}, and there exists an angle, θ′\theta', between them. We can split R′\mathbf{R'} into the parts of the ray that are perpendicular to n′\mathbf{n'} and parallel to n′\mathbf{n'}:

R′=R′⊥+R′∥\mathbf{R'} = \mathbf{R'}_{\bot} + \mathbf{R'}_{\parallel}

If we solve for R′⊥\mathbf{R'}_{\bot} and R′∥\mathbf{R'}_{\parallel} we get:

R′⊥=ηη′(R+cos⁡θn)\mathbf{R'}_{\bot} = \frac{\eta}{\eta'} (\mathbf{R} + \cos\theta \mathbf{n})
R′∥=−1−∣R′⊥∣2n\mathbf{R'}_{\parallel} = -\sqrt{1 - |\mathbf{R'}_{\bot}|^2} \mathbf{n}

You can go ahead and prove this for yourself if you want, but we will treat it as fact and move on. The rest of the book will not require you to understand the proof.

We still need to solve for cos⁡θ\cos\theta. It is well known that the dot product of two vectors can be explained in terms of the cosine of the angle between them:

a⋅b=∣a∣∣b∣cos⁡θ\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos\theta

If we restrict a\mathbf{a} and b\mathbf{b} to be unit vectors:

a⋅b=cos⁡θ\mathbf{a} \cdot \mathbf{b} = \cos\theta

We can now rewrite R′⊥\mathbf{R'}_{\bot} in terms of known quantities:

R′⊥=ηη′(R+(−R⋅n)n)\mathbf{R'}_{\bot} = \frac{\eta}{\eta'} (\mathbf{R} + (\mathbf{-R} \cdot \mathbf{n}) \mathbf{n})

When we combine them back together, we can write a function to calculate R′\mathbf{R'}:

vec3.rs | Refraction function
use std::fmt::{Display, Formatter, Result};
use std::ops::{Add, AddAssign, Div, DivAssign, Mul, MulAssign, Neg, Sub};
 
use crate::common;
 
#[derive(Copy, Clone, Default)]
pub struct Vec3 {
    e: [f64; 3],
}
 
impl Vec3 {
    pub fn new(x: f64, y: f64, z: f64) -> Vec3 {
        Vec3 { e: [x, y, z] }
    }
 
    pub fn random() -> Vec3 {
        Vec3::new(
            common::random_double(),
            common::random_double(),
            common::random_double(),
        )
    }
 
    pub fn random_range(min: f64, max: f64) -> Vec3 {
        Vec3::new(
            common::random_double_range(min, max),
            common::random_double_range(min, max),
            common::random_double_range(min, max),
        )
    }
 
    pub fn x(&self) -> f64 {
        self.e[0]
    }
 
    pub fn y(&self) -> f64 {
        self.e[1]
    }
 
    pub fn z(&self) -> f64 {
        self.e[2]
    }
 
    pub fn length(&self) -> f64 {
        f64::sqrt(self.length_squared())
    }
 
    pub fn length_squared(&self) -> f64 {
        self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
    }
 
    pub fn near_zero(&self) -> bool {
        const EPS: f64 = 1.0e-8;
        // Return true if the vector is close to zero in all dimensions
        self.e[0].abs() < EPS && self.e[1].abs() < EPS && self.e[2].abs() < EPS
    }
}
 
// Type alias
pub type Point3 = Vec3;
 
// Output formatting
impl Display for Vec3 {
    fn fmt(&self, f: &mut Formatter) -> Result {
        write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
    }
}
 
// -Vec3
impl Neg for Vec3 {
    type Output = Vec3;
 
    fn neg(self) -> Vec3 {
        Vec3::new(-self.x(), -self.y(), -self.z())
    }
}
 
// Vec3 += Vec3
impl AddAssign for Vec3 {
    fn add_assign(&mut self, v: Vec3) {
        *self = *self + v;
    }
}
 
// Vec3 *= f64
impl MulAssign<f64> for Vec3 {
    fn mul_assign(&mut self, t: f64) {
        *self = *self * t;
    }
}
 
// Vec3 /= f64
impl DivAssign<f64> for Vec3 {
    fn div_assign(&mut self, t: f64) {
        *self = *self / t;
    }
}
 
// Vec3 + Vec3
impl Add for Vec3 {
    type Output = Vec3;
 
    fn add(self, v: Vec3) -> Vec3 {
        Vec3::new(self.x() + v.x(), self.y() + v.y(), self.z() + v.z())
    }
}
 
// Vec3 - Vec3
impl Sub for Vec3 {
    type Output = Vec3;
 
    fn sub(self, v: Vec3) -> Vec3 {
        Vec3::new(self.x() - v.x(), self.y() - v.y(), self.z() - v.z())
    }
}
 
// Vec3 * Vec3
impl Mul for Vec3 {
    type Output = Vec3;
 
    fn mul(self, v: Vec3) -> Vec3 {
        Vec3::new(self.x() * v.x(), self.y() * v.y(), self.z() * v.z())
    }
}
 
// f64 * Vec3
impl Mul<Vec3> for f64 {
    type Output = Vec3;
 
    fn mul(self, v: Vec3) -> Vec3 {
        Vec3::new(self * v.x(), self * v.y(), self * v.z())
    }
}
 
// Vec3 * f64
impl Mul<f64> for Vec3 {
    type Output = Vec3;
 
    fn mul(self, t: f64) -> Vec3 {
        Vec3::new(self.x() * t, self.y() * t, self.z() * t)
    }
}
 
// Vec3 / f64
impl Div<f64> for Vec3 {
    type Output = Vec3;
 
    fn div(self, t: f64) -> Vec3 {
        Vec3::new(self.x() / t, self.y() / t, self.z() / t)
    }
}
 
pub fn dot(u: Vec3, v: Vec3) -> f64 {
    u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
}
 
pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
    Vec3::new(
        u.e[1] * v.e[2] - u.e[2] * v.e[1],
        u.e[2] * v.e[0] - u.e[0] * v.e[2],
        u.e[0] * v.e[1] - u.e[1] * v.e[0],
    )
}
 
pub fn unit_vector(v: Vec3) -> Vec3 {
    v / v.length()
}
 
pub fn random_in_unit_sphere() -> Vec3 {
    loop {
        let p = Vec3::random_range(-1.0, 1.0);
        if p.length_squared() >= 1.0 {
            continue;
        }
        return p;
    }
}
 
pub fn random_unit_vector() -> Vec3 {
    unit_vector(random_in_unit_sphere())
}
 
pub fn reflect(v: Vec3, n: Vec3) -> Vec3 {
    v - 2.0 * dot(v, n) * n
}
 
pub fn refract(uv: Vec3, n: Vec3, etai_over_etat: f64) -> Vec3 {
    let cos_theta = f64::min(dot(-uv, n), 1.0);
    let r_out_perp = etai_over_etat * (uv + cos_theta * n);
    let r_out_parallel = -f64::sqrt(f64::abs(1.0 - r_out_perp.length_squared())) * n;
    r_out_perp + r_out_parallel
}

And the dielectric material that always refracts is:

material.rs | Dielectric Material struct that always refracts
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
use crate::vec3;
 
pub trait Material {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool;
}
 
pub struct Lambertian {
    albedo: Color,
}
 
impl Lambertian {
    pub fn new(a: Color) -> Lambertian {
        Lambertian { albedo: a }
    }
}
 
impl Material for Lambertian {
    fn scatter(
        &self,
        _r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let mut scatter_direction = rec.normal + vec3::random_unit_vector();
 
        // Catch degenerate scatter direction
        if scatter_direction.near_zero() {
            scatter_direction = rec.normal;
        }
 
        *attenuation = self.albedo;
        *scattered = Ray::new(rec.p, scatter_direction);
        true
    }
}
 
pub struct Metal {
    albedo: Color,
    fuzz: f64,
}
 
impl Metal {
    pub fn new(a: Color, f: f64) -> Metal {
        Metal {
            albedo: a,
            fuzz: if f < 1.0 { f } else { 1.0 },
        }
    }
}
 
impl Material for Metal {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let reflected = vec3::reflect(vec3::unit_vector(r_in.direction()), rec.normal);
 
        *attenuation = self.albedo;
        *scattered = Ray::new(rec.p, reflected + self.fuzz * vec3::random_in_unit_sphere());
        vec3::dot(scattered.direction(), rec.normal) > 0.0
    }
}
 
pub struct Dielectric {
    ir: f64, // Index of refraction
}
 
impl Dielectric {
    pub fn new(index_of_refraction: f64) -> Dielectric {
        Dielectric {
            ir: index_of_refraction,
        }
    }
}
 
impl Material for Dielectric {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let refraction_ratio = if rec.front_face {
            1.0 / self.ir
        } else {
            self.ir
        };
 
        let unit_direction = vec3::unit_vector(r_in.direction());
        let refracted = vec3::refract(unit_direction, rec.normal, refraction_ratio);
 
        *attenuation = Color::new(1.0, 1.0, 1.0);
        *scattered = Ray::new(rec.p, refracted);
        true
    }
}

Now we’ll update the scene to change the left and center spheres to glass:

main.rs | Changing left and center spheres to glass
mod camera;
mod color;
mod common;
mod hittable;
mod hittable_list;
mod material;
mod ray;
mod sphere;
mod vec3;
 
use std::io;
use std::rc::Rc;
 
use camera::Camera;
use color::Color;
use hittable::{HitRecord, Hittable};
use hittable_list::HittableList;
use material::{Dielectric, Lambertian, Metal};
use ray::Ray;
use sphere::Sphere;
use vec3::Point3;
 
fn ray_color(r: &Ray, world: &dyn Hittable, depth: i32) -> Color {
    // If we've exceeded the ray bounce limit, no more light is gathered
    if depth <= 0 {
        return Color::new(0.0, 0.0, 0.0);
    }
 
    let mut rec = HitRecord::new();
    if world.hit(r, 0.001, common::INFINITY, &mut rec) {
        let mut attenuation = Color::default();
        let mut scattered = Ray::default();
        if rec
            .mat
            .as_ref()
            .unwrap()
            .scatter(r, &rec, &mut attenuation, &mut scattered)
        {
            return attenuation * ray_color(&scattered, world, depth - 1);
        }
        return Color::new(0.0, 0.0, 0.0);
    }
 
    let unit_direction = vec3::unit_vector(r.direction());
    let t = 0.5 * (unit_direction.y() + 1.0);
    (1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
 
fn main() {
    // Image
 
    const ASPECT_RATIO: f64 = 16.0 / 9.0;
    const IMAGE_WIDTH: i32 = 400;
    const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
    const SAMPLES_PER_PIXEL: i32 = 100;
    const MAX_DEPTH: i32 = 50;
 
    // World
 
    let mut world = HittableList::new();
 
    let material_ground = Rc::new(Lambertian::new(Color::new(0.8, 0.8, 0.0)));
    let material_center = Rc::new(Dielectric::new(1.5));
    let material_left = Rc::new(Dielectric::new(1.5));
    let material_right = Rc::new(Metal::new(Color::new(0.8, 0.6, 0.2), 1.0));
 
    world.add(Box::new(Sphere::new(
        Point3::new(0.0, -100.5, -1.0),
        100.0,
        material_ground,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(0.0, 0.0, -1.0),
        0.5,
        material_center,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(-1.0, 0.0, -1.0),
        0.5,
        material_left,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(1.0, 0.0, -1.0),
        0.5,
        material_right,
    )));
 
    // Camera
 
    let cam = Camera::new();
 
    // Render
 
    print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
 
    for j in (0..IMAGE_HEIGHT).rev() {
        eprint!("\rScanlines remaining: {} ", j);
        for i in 0..IMAGE_WIDTH {
            let mut pixel_color = Color::new(0.0, 0.0, 0.0);
            for _ in 0..SAMPLES_PER_PIXEL {
                let u = (i as f64 + common::random_double()) / (IMAGE_WIDTH - 1) as f64;
                let v = (j as f64 + common::random_double()) / (IMAGE_HEIGHT - 1) as f64;
                let r = cam.get_ray(u, v);
                pixel_color += ray_color(&r, &world, MAX_DEPTH);
            }
            color::write_color(&mut io::stdout(), pixel_color, SAMPLES_PER_PIXEL);
        }
    }
 
    eprint!("\nDone.\n");
}

This gives us the following result:

Glass sphere that always refracts
Glass sphere that always refracts

Total Internal Reflection

That definitely doesn’t look right. One troublesome practical issue is that when the ray is in the material with the higher refractive index, there is no real solution to Snell’s law, and thus there is no refraction possible. If we refer back to Snell’s law and the derivation of sin⁡θ′\sin\theta':

sin⁡θ′=ηη′⋅sin⁡θ\sin\theta' = \frac{\eta}{\eta'} \cdot \sin\theta

If the ray is inside glass and outside is air (η=1.5\eta = 1.5 and η′=1.0\eta' = 1.0):

sin⁡θ′=1.51.0⋅sin⁡θ\sin\theta' = \frac{1.5}{1.0} \cdot \sin\theta

The value of sin⁡θ′\sin\theta' cannot be greater than 1. So, if,

1.51.0⋅sin⁡θ>1.0\frac{1.5}{1.0} \cdot \sin\theta > 1.0

the equality between the two sides of the equation is broken, and a solution cannot exist. If a solution does not exist, the glass cannot refract, and therefore must reflect the ray. Here all the light is reflected. It is called “total internal reflection” because in practice that is usually inside solid objects. This is why sometimes the water-air boundary acts as a perfect mirror when you are submerged.

We can solve for sin_theta using the trigonometric qualities:

sin⁡θ=1−cos⁡2θ\sin\theta = \sqrt{1 - \cos^2\theta}

and

cos⁡θ=R⋅n\cos\theta = \mathbf{R} \cdot \mathbf{n}

And the dielectric material that always refracts when possible is:

material.rs | Dielectric Material struct with reflection
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
use crate::vec3;
 
pub trait Material {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool;
}
 
pub struct Lambertian {
    albedo: Color,
}
 
impl Lambertian {
    pub fn new(a: Color) -> Lambertian {
        Lambertian { albedo: a }
    }
}
 
impl Material for Lambertian {
    fn scatter(
        &self,
        _r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let mut scatter_direction = rec.normal + vec3::random_unit_vector();
 
        // Catch degenerate scatter direction
        if scatter_direction.near_zero() {
            scatter_direction = rec.normal;
        }
 
        *attenuation = self.albedo;
        *scattered = Ray::new(rec.p, scatter_direction);
        true
    }
}
 
pub struct Metal {
    albedo: Color,
    fuzz: f64,
}
 
impl Metal {
    pub fn new(a: Color, f: f64) -> Metal {
        Metal {
            albedo: a,
            fuzz: if f < 1.0 { f } else { 1.0 },
        }
    }
}
 
impl Material for Metal {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let reflected = vec3::reflect(vec3::unit_vector(r_in.direction()), rec.normal);
 
        *attenuation = self.albedo;
        *scattered = Ray::new(rec.p, reflected + self.fuzz * vec3::random_in_unit_sphere());
        vec3::dot(scattered.direction(), rec.normal) > 0.0
    }
}
 
pub struct Dielectric {
    ir: f64, // Index of refraction
}
 
impl Dielectric {
    pub fn new(index_of_refraction: f64) -> Dielectric {
        Dielectric {
            ir: index_of_refraction,
        }
    }
}
 
impl Material for Dielectric {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let refraction_ratio = if rec.front_face {
            1.0 / self.ir
        } else {
            self.ir
        };
 
        let unit_direction = vec3::unit_vector(r_in.direction());
        let cos_theta = f64::min(vec3::dot(-unit_direction, rec.normal), 1.0);
        let sin_theta = f64::sqrt(1.0 - cos_theta * cos_theta);
 
        let cannot_refract = refraction_ratio * sin_theta > 1.0;
        let direction = if cannot_refract {
            vec3::reflect(unit_direction, rec.normal)
        } else {
            vec3::refract(unit_direction, rec.normal, refraction_ratio)
        };
 
        *attenuation = Color::new(1.0, 1.0, 1.0);
        *scattered = Ray::new(rec.p, direction);
        true
    }
}

Attenuation is always 1 — the glass surface absorbs nothing. If we try that out with these parameters:

main.rs | Scene with dielectric and shiny sphere
mod camera;
mod color;
mod common;
mod hittable;
mod hittable_list;
mod material;
mod ray;
mod sphere;
mod vec3;
 
use std::io;
use std::rc::Rc;
 
use camera::Camera;
use color::Color;
use hittable::{HitRecord, Hittable};
use hittable_list::HittableList;
use material::{Dielectric, Lambertian, Metal};
use ray::Ray;
use sphere::Sphere;
use vec3::Point3;
 
fn ray_color(r: &Ray, world: &dyn Hittable, depth: i32) -> Color {
    // If we've exceeded the ray bounce limit, no more light is gathered
    if depth <= 0 {
        return Color::new(0.0, 0.0, 0.0);
    }
 
    let mut rec = HitRecord::new();
    if world.hit(r, 0.001, common::INFINITY, &mut rec) {
        let mut attenuation = Color::default();
        let mut scattered = Ray::default();
        if rec
            .mat
            .as_ref()
            .unwrap()
            .scatter(r, &rec, &mut attenuation, &mut scattered)
        {
            return attenuation * ray_color(&scattered, world, depth - 1);
        }
        return Color::new(0.0, 0.0, 0.0);
    }
 
    let unit_direction = vec3::unit_vector(r.direction());
    let t = 0.5 * (unit_direction.y() + 1.0);
    (1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
 
fn main() {
    // Image
 
    const ASPECT_RATIO: f64 = 16.0 / 9.0;
    const IMAGE_WIDTH: i32 = 400;
    const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
    const SAMPLES_PER_PIXEL: i32 = 100;
    const MAX_DEPTH: i32 = 50;
 
    // World
 
    let mut world = HittableList::new();
 
    let material_ground = Rc::new(Lambertian::new(Color::new(0.8, 0.8, 0.0)));
    let material_center = Rc::new(Lambertian::new(Color::new(0.1, 0.2, 0.5)));
    let material_left = Rc::new(Dielectric::new(1.5));
    let material_right = Rc::new(Metal::new(Color::new(0.8, 0.6, 0.2), 0.0));
 
    world.add(Box::new(Sphere::new(
        Point3::new(0.0, -100.5, -1.0),
        100.0,
        material_ground,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(0.0, 0.0, -1.0),
        0.5,
        material_center,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(-1.0, 0.0, -1.0),
        0.5,
        material_left,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(1.0, 0.0, -1.0),
        0.5,
        material_right,
    )));
 
    // Camera
 
    let cam = Camera::new();
 
    // Render
 
    print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
 
    for j in (0..IMAGE_HEIGHT).rev() {
        eprint!("\rScanlines remaining: {} ", j);
        for i in 0..IMAGE_WIDTH {
            let mut pixel_color = Color::new(0.0, 0.0, 0.0);
            for _ in 0..SAMPLES_PER_PIXEL {
                let u = (i as f64 + common::random_double()) / (IMAGE_WIDTH - 1) as f64;
                let v = (j as f64 + common::random_double()) / (IMAGE_HEIGHT - 1) as f64;
                let r = cam.get_ray(u, v);
                pixel_color += ray_color(&r, &world, MAX_DEPTH);
            }
            color::write_color(&mut io::stdout(), pixel_color, SAMPLES_PER_PIXEL);
        }
    }
 
    eprint!("\nDone.\n");
}

We get:

Glass sphere that sometimes refracts
Glass sphere that sometimes refracts

Schlick Approximation

Now real glass has reflectivity that varies with angle — look at a window at a steep angle and it becomes a mirror. There is a big ugly equation for that, but almost everybody uses a cheap and surprisingly accurate polynomial approximation by Christophe Schlick. This yields our full glass material:

material.rs | Full glass material
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
use crate::{common, vec3};
 
pub trait Material {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool;
}
 
pub struct Lambertian {
    albedo: Color,
}
 
impl Lambertian {
    pub fn new(a: Color) -> Lambertian {
        Lambertian { albedo: a }
    }
}
 
impl Material for Lambertian {
    fn scatter(
        &self,
        _r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let mut scatter_direction = rec.normal + vec3::random_unit_vector();
 
        // Catch degenerate scatter direction
        if scatter_direction.near_zero() {
            scatter_direction = rec.normal;
        }
 
        *attenuation = self.albedo;
        *scattered = Ray::new(rec.p, scatter_direction);
        true
    }
}
 
pub struct Metal {
    albedo: Color,
    fuzz: f64,
}
 
impl Metal {
    pub fn new(a: Color, f: f64) -> Metal {
        Metal {
            albedo: a,
            fuzz: if f < 1.0 { f } else { 1.0 },
        }
    }
}
 
impl Material for Metal {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let reflected = vec3::reflect(vec3::unit_vector(r_in.direction()), rec.normal);
 
        *attenuation = self.albedo;
        *scattered = Ray::new(rec.p, reflected + self.fuzz * vec3::random_in_unit_sphere());
        vec3::dot(scattered.direction(), rec.normal) > 0.0
    }
}
 
pub struct Dielectric {
    ir: f64, // Index of refraction
}
 
impl Dielectric {
    pub fn new(index_of_refraction: f64) -> Dielectric {
        Dielectric {
            ir: index_of_refraction,
        }
    }
 
    fn reflectance(cosine: f64, ref_idx: f64) -> f64 {
        // Use Schlick's approximation for reflectance
        let mut r0 = (1.0 - ref_idx) / (1.0 + ref_idx);
        r0 = r0 * r0;
        r0 + (1.0 - r0) * f64::powf(1.0 - cosine, 5.0)
    }
}
 
impl Material for Dielectric {
    fn scatter(
        &self,
        r_in: &Ray,
        rec: &HitRecord,
        attenuation: &mut Color,
        scattered: &mut Ray,
    ) -> bool {
        let refraction_ratio = if rec.front_face {
            1.0 / self.ir
        } else {
            self.ir
        };
 
        let unit_direction = vec3::unit_vector(r_in.direction());
        let cos_theta = f64::min(vec3::dot(-unit_direction, rec.normal), 1.0);
        let sin_theta = f64::sqrt(1.0 - cos_theta * cos_theta);
 
        let cannot_refract = refraction_ratio * sin_theta > 1.0;
        let direction = if cannot_refract
            || Self::reflectance(cos_theta, refraction_ratio) > common::random_double()
        {
            vec3::reflect(unit_direction, rec.normal)
        } else {
            vec3::refract(unit_direction, rec.normal, refraction_ratio)
        };
 
        *attenuation = Color::new(1.0, 1.0, 1.0);
        *scattered = Ray::new(rec.p, direction);
        true
    }
}

Modeling a Hollow Glass Sphere

An interesting and easy trick with dielectric spheres is to note that if you use a negative radius, the geometry is unaffected, but the surface normal points inward. This can be used as a bubble to make a hollow glass sphere:

main.rs | Scene with hollow glass sphere
mod camera;
mod color;
mod common;
mod hittable;
mod hittable_list;
mod material;
mod ray;
mod sphere;
mod vec3;
 
use std::io;
use std::rc::Rc;
 
use camera::Camera;
use color::Color;
use hittable::{HitRecord, Hittable};
use hittable_list::HittableList;
use material::{Dielectric, Lambertian, Metal};
use ray::Ray;
use sphere::Sphere;
use vec3::Point3;
 
fn ray_color(r: &Ray, world: &dyn Hittable, depth: i32) -> Color {
    // If we've exceeded the ray bounce limit, no more light is gathered
    if depth <= 0 {
        return Color::new(0.0, 0.0, 0.0);
    }
 
    let mut rec = HitRecord::new();
    if world.hit(r, 0.001, common::INFINITY, &mut rec) {
        let mut attenuation = Color::default();
        let mut scattered = Ray::default();
        if rec
            .mat
            .as_ref()
            .unwrap()
            .scatter(r, &rec, &mut attenuation, &mut scattered)
        {
            return attenuation * ray_color(&scattered, world, depth - 1);
        }
        return Color::new(0.0, 0.0, 0.0);
    }
 
    let unit_direction = vec3::unit_vector(r.direction());
    let t = 0.5 * (unit_direction.y() + 1.0);
    (1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
 
fn main() {
    // Image
 
    const ASPECT_RATIO: f64 = 16.0 / 9.0;
    const IMAGE_WIDTH: i32 = 400;
    const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
    const SAMPLES_PER_PIXEL: i32 = 100;
    const MAX_DEPTH: i32 = 50;
 
    // World
 
    let mut world = HittableList::new();
 
    let material_ground = Rc::new(Lambertian::new(Color::new(0.8, 0.8, 0.0)));
    let material_center = Rc::new(Lambertian::new(Color::new(0.1, 0.2, 0.5)));
    let material_left = Rc::new(Dielectric::new(1.5));
    let material_right = Rc::new(Metal::new(Color::new(0.8, 0.6, 0.2), 0.0));
 
    world.add(Box::new(Sphere::new(
        Point3::new(0.0, -100.5, -1.0),
        100.0,
        material_ground,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(0.0, 0.0, -1.0),
        0.5,
        material_center,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(-1.0, 0.0, -1.0),
        0.5,
        material_left.clone(),
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(-1.0, 0.0, -1.0),
        -0.4,
        material_left,
    )));
    world.add(Box::new(Sphere::new(
        Point3::new(1.0, 0.0, -1.0),
        0.5,
        material_right,
    )));
 
    // Camera
 
    let cam = Camera::new();
 
    // Render
 
    print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
 
    for j in (0..IMAGE_HEIGHT).rev() {
        eprint!("\rScanlines remaining: {} ", j);
        for i in 0..IMAGE_WIDTH {
            let mut pixel_color = Color::new(0.0, 0.0, 0.0);
            for _ in 0..SAMPLES_PER_PIXEL {
                let u = (i as f64 + common::random_double()) / (IMAGE_WIDTH - 1) as f64;
                let v = (j as f64 + common::random_double()) / (IMAGE_HEIGHT - 1) as f64;
                let r = cam.get_ray(u, v);
                pixel_color += ray_color(&r, &world, MAX_DEPTH);
            }
            color::write_color(&mut io::stdout(), pixel_color, SAMPLES_PER_PIXEL);
        }
    }
 
    eprint!("\nDone.\n");
}

This gives:

A hollow glass sphere
A hollow glass sphere
9. Metal11. Positionable Camera