Surface Normals and Multiple Objects

Shading with Surface Normals

First, let’s get ourselves a surface normal so we can shade. This is a vector that is perpendicular to the surface at the point of intersection. We have a design decision to make: whether these normals are unit length. Because that is convenient for shading, we will make it unit length.

For a sphere, the outward normal is in the direction of the hit point minus the center:

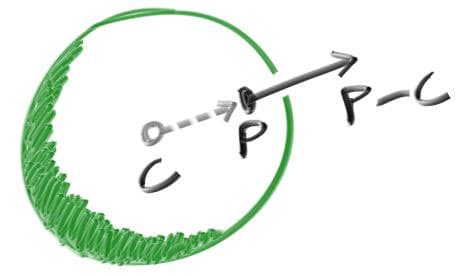
On the earth, this implies that the vector from the earth’s center to you points straight up. Let’s throw that into the code now, and shade it. We don’t have any lights or anything yet, so let’s just visualize the normals with a color map.

A common trick used for visualizing normals (because it’s easy and somewhat intuitive to assume $\mathbf{n}$ is a unit length vector — so each component is between -1 and 1) is to map each component to the interval from 0 to 1, and then map (x, y, z) to (r, g, b). For the normal, we need the hit point, not just whether we hit or not. We only have one sphere in the scene, and it’s directly in front of the camera, so we won’t worry about negative values of $t$ yet. We’ll just assume the closest hit point (smallest $t$ ):

t = \frac{-b - \sqrt{b^2 - 4ac}}{2a}

These changes in the code let us compute and visualize $\mathbf{n}$ :

main.rs | Rendering surface normals on a sphere

mod color;
mod ray;
mod vec3;
 
use std::io;
 
use color::Color;
use ray::Ray;
use vec3::{Point3, Vec3};
 
fn hit_sphere(center: Point3, radius: f64, r: &Ray) -> f64 {
    let oc = r.origin() - center;
    let a = vec3::dot(r.direction(), r.direction());
    let b = 2.0 * vec3::dot(oc, r.direction());
    let c = vec3::dot(oc, oc) - radius * radius;
    let discriminant = b * b - 4.0 * a * c;
    if discriminant < 0.0 {
        -1.0
    } else {
        (-b - f64::sqrt(discriminant)) / (2.0 * a)
    }
}
 
fn ray_color(r: &Ray) -> Color {
    let t = hit_sphere(Point3::new(0.0, 0.0, -1.0), 0.5, r);
    if t > 0.0 {
        let n = vec3::unit_vector(r.at(t) - Vec3::new(0.0, 0.0, -1.0));
        return 0.5 * Color::new(n.x() + 1.0, n.y() + 1.0, n.z() + 1.0);
    }
 
    let unit_direction = vec3::unit_vector(r.direction());
    let t = 0.5 * (unit_direction.y() + 1.0);
    (1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
 
fn main() {
    // Image
 
    const ASPECT_RATIO: f64 = 16.0 / 9.0;
    const IMAGE_WIDTH: i32 = 400;
    const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
 
    // Camera
 
    let viewport_height = 2.0;
    let viewport_width = ASPECT_RATIO * viewport_height;
    let focal_length = 1.0;
 
    let origin = Point3::new(0.0, 0.0, 0.0);
    let horizontal = Vec3::new(viewport_width, 0.0, 0.0);
    let vertical = Vec3::new(0.0, viewport_height, 0.0);
    let lower_left_corner =
        origin - horizontal / 2.0 - vertical / 2.0 - Vec3::new(0.0, 0.0, focal_length);
 
    // Render
 
    print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
 
    for j in (0..IMAGE_HEIGHT).rev() {
        eprint!("\rScanlines remaining: {} ", j);
        for i in 0..IMAGE_WIDTH {
            let u = i as f64 / (IMAGE_WIDTH - 1) as f64;
            let v = j as f64 / (IMAGE_HEIGHT - 1) as f64;
            let r = Ray::new(
                origin,
                lower_left_corner + u * horizontal + v * vertical - origin,
            );
            let pixel_color = ray_color(&r);
            color::write_color(&mut io::stdout(), pixel_color);
        }
    }
 
    eprint!("\nDone.\n");
}

And that yields this picture:

A sphere colored according to its normal vectors

Simplifying the Ray-Sphere Intersection Code

Let’s revisit the ray-sphere equation:

t = \frac{-b - \sqrt{b^2 - 4ac}}{2a}

First, recall that a vector dotted with itself is equal to the squared length of that vector. Second, notice how the equation for b has a factor of two in it. Consider what happens to the quadratic equation if $b = 2h$ :

t = \frac{-b - \sqrt{b^2 - 4ac}}{2a}

= \frac{-2h - \sqrt{(2h)^2 - 4ac}}{2a}

= \frac{-2h - 2\sqrt{h^2 - ac}}{2a}

= \frac{-h - \sqrt{h^2 - ac}}{a}

Using these observations, we can now simplify the sphere-intersection code to this:

main.rs | Ray-sphere intersection code (after)

mod color;
mod ray;
mod vec3;
 
use std::io;
 
use color::Color;
use ray::Ray;
use vec3::{Point3, Vec3};
 
fn hit_sphere(center: Point3, radius: f64, r: &Ray) -> f64 {
    let oc = r.origin() - center;
    let a = r.direction().length_squared();
    let half_b = vec3::dot(oc, r.direction());
    let c = oc.length_squared() - radius * radius;
    let discriminant = half_b * half_b - a * c;
    if discriminant < 0.0 {
        -1.0
    } else {
        (-half_b - f64::sqrt(discriminant)) / a
    }
}
 
fn ray_color(r: &Ray) -> Color {
    let t = hit_sphere(Point3::new(0.0, 0.0, -1.0), 0.5, r);
    if t > 0.0 {
        let n = vec3::unit_vector(r.at(t) - Vec3::new(0.0, 0.0, -1.0));
        return 0.5 * Color::new(n.x() + 1.0, n.y() + 1.0, n.z() + 1.0);
    }
 
    let unit_direction = vec3::unit_vector(r.direction());
    let t = 0.5 * (unit_direction.y() + 1.0);
    (1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
 
fn main() {
    // Image
 
    const ASPECT_RATIO: f64 = 16.0 / 9.0;
    const IMAGE_WIDTH: i32 = 400;
    const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
 
    // Camera
 
    let viewport_height = 2.0;
    let viewport_width = ASPECT_RATIO * viewport_height;
    let focal_length = 1.0;
 
    let origin = Point3::new(0.0, 0.0, 0.0);
    let horizontal = Vec3::new(viewport_width, 0.0, 0.0);
    let vertical = Vec3::new(0.0, viewport_height, 0.0);
    let lower_left_corner =
        origin - horizontal / 2.0 - vertical / 2.0 - Vec3::new(0.0, 0.0, focal_length);
 
    // Render
 
    print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
 
    for j in (0..IMAGE_HEIGHT).rev() {
        eprint!("\rScanlines remaining: {} ", j);
        for i in 0..IMAGE_WIDTH {
            let u = i as f64 / (IMAGE_WIDTH - 1) as f64;
            let v = j as f64 / (IMAGE_HEIGHT - 1) as f64;
            let r = Ray::new(
                origin,
                lower_left_corner + u * horizontal + v * vertical - origin,
            );
            let pixel_color = ray_color(&r);
            color::write_color(&mut io::stdout(), pixel_color);
        }
    }
 
    eprint!("\nDone.\n");
}

An Abstraction for Hittable Objects

Now, how about several spheres? While it is tempting to have an array of spheres, a very clean solution is the make a common interface for anything a ray might hit, and make both a sphere and a list of spheres just something you can hit. In Rust, we can define the common interface through a feature called “trait.” We will called the trait Hittable.

This Hittable trait will have a hit function that takes in a ray. Most ray tracers have found it convenient to add a valid interval for hits $t_{min}$ to $t_{max}$ , so the hit only “counts” if $t_{min} < t < t_{max}$ . For the initial rays this is positive $t$ , but as we will see, it can help some details in the code to have an interval $t_{min}$ to $t_{max}$ .

One design question is whether to do things like compute the normal if we hit something. We might end up hitting something closer as we do our search, and we will only need the normal of the closest thing. We will go with the simple solution and compute a bundle of stuff in a struct called HitRecord.

Here’s the code:

hittable.rs | The Hittable trait

use crate::ray::Ray;
use crate::vec3::{self, Point3, Vec3};
 
#[derive(Clone, Default)]
pub struct HitRecord {
    pub p: Point3,
    pub normal: Vec3,
    pub t: f64,
}
 
impl HitRecord {
    pub fn new() -> HitRecord {
        Default::default()
    }
}
 
pub trait Hittable {
    fn hit(&self, ray: &Ray, t_min: f64, t_max: f64, rec: &mut HitRecord) -> bool;
}

And here’s the sphere:

sphere.rs | The Sphere struct

use crate::hittable::{HitRecord, Hittable};
use crate::ray::Ray;
use crate::vec3::{self, Point3};
 
pub struct Sphere {
    center: Point3,
    radius: f64,
}
 
impl Sphere {
    pub fn new(cen: Point3, r: f64) -> Sphere {
        Sphere {
            center: cen,
            radius: r,
        }
    }
}
 
impl Hittable for Sphere {
    fn hit(&self, r: &Ray, t_min: f64, t_max: f64, rec: &mut HitRecord) -> bool {
        let oc = r.origin() - self.center;
        let a = r.direction().length_squared();
        let half_b = vec3::dot(oc, r.direction());
        let c = oc.length_squared() - self.radius * self.radius;
        let discriminant = half_b * half_b - a * c;
        if discriminant < 0.0 {
            return false;
        }
 
        let sqrt_d = f64::sqrt(discriminant);
 
        // Find the nearest root that lies in the acceptable range
        let mut root = (-half_b - sqrt_d) / a;
        if root <= t_min || t_max <= root {
            root = (-half_b + sqrt_d) / a;
            if root <= t_min || t_max <= root {
                return false;
            }
        }
 
        rec.t = root;
        rec.p = r.at(rec.t);
        rec.normal = (rec.p - center) / radius;
        true
    }
}

Front Faces Versus Back Faces

Another design decision for storing normals in HitRecord is whether they should always point outward or they should points against the incident ray.

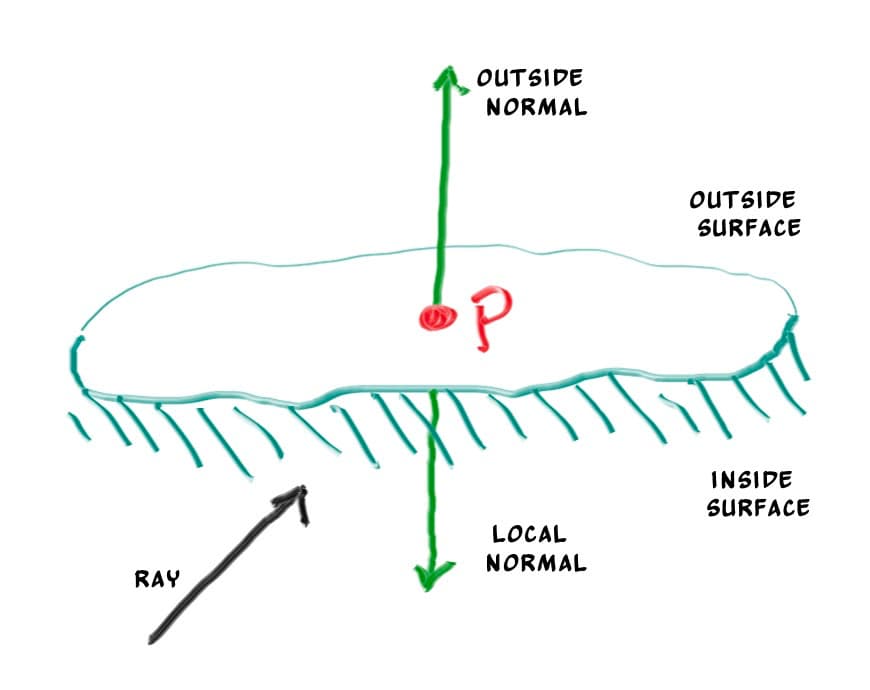
Possible directions for sphere surface-normal geometry

We need to choose one of these possibilities because we will eventually want to determine which side of the surface that the ray is coming from. This is important for objects that are rendered differently on each side, like the text on a two-sided sheet of paper, or for objects that have an inside and an outside, like glass balls.

This decision is determined by whether you want to determine the side of the surface at the time of geometry intersection or at the time of coloring. In this book we have more material types than we have geometry types, so we’ll put the determination at geometry time, i.e., making the normal always point against the ray. This is simply a matter of preference, and you’ll see both implementations in the literature.

We’ll add the front_face bool to the HitRecord struct. We’ll also add a set_face_normal() function to solve the calculation by taking the dot product of the ray direction and the outward normal of the sphere (in the direction of the center to the intersection point). If the product is negative, the ray is from the outside. Otherwise, it is from the inside.

Here is the code:

hittable.rs | Adding front-face tracking to HitRecord

use crate::ray::Ray;
use crate::vec3::{self, Point3, Vec3};
 
#[derive(Clone, Default)]
pub struct HitRecord {
    pub p: Point3,
    pub normal: Vec3,
    pub t: f64,
    pub front_face: bool,
}
 
impl HitRecord {
    pub fn new() -> HitRecord {
        Default::default()
    }
 
    pub fn set_face_normal(&mut self, r: &Ray, outward_normal: Vec3) {
        self.front_face = vec3::dot(r.direction(), outward_normal) < 0.0;
        self.normal = if self.front_face {
            outward_normal
        } else {
            -outward_normal
        };
    }
}
 
pub trait Hittable {
    fn hit(&self, ray: &Ray, t_min: f64, t_max: f64, rec: &mut HitRecord) -> bool;
}

And then we add the surface side determination to the struct:

sphere.rs | The Sphere struct with normal determination

use crate::hittable::{HitRecord, Hittable};
use crate::ray::Ray;
use crate::vec3::{self, Point3};
 
pub struct Sphere {
    center: Point3,
    radius: f64,
}
 
impl Sphere {
    pub fn new(cen: Point3, r: f64) -> Sphere {
        Sphere {
            center: cen,
            radius: r,
        }
    }
}
 
impl Hittable for Sphere {
    fn hit(&self, r: &Ray, t_min: f64, t_max: f64, rec: &mut HitRecord) -> bool {
        let oc = r.origin() - self.center;
        let a = r.direction().length_squared();
        let half_b = vec3::dot(oc, r.direction());
        let c = oc.length_squared() - self.radius * self.radius;
        let discriminant = half_b * half_b - a * c;
        if discriminant < 0.0 {
            return false;
        }
 
        let sqrt_d = f64::sqrt(discriminant);
 
        // Find the nearest root that lies in the acceptable range
        let mut root = (-half_b - sqrt_d) / a;
        if root <= t_min || t_max <= root {
            root = (-half_b + sqrt_d) / a;
            if root <= t_min || t_max <= root {
                return false;
            }
        }
 
        rec.t = root;
        rec.p = r.at(rec.t);
        let outward_normal = (rec.p - self.center) / self.radius;
        rec.set_face_normal(r, outward_normal);
        true
    }
}

A List of Hittable Objects

We now add a HittableList struct that stores a list of Hittable trait objects.

hittable_list.rs | The HittableList struct

use crate::hittable::{HitRecord, Hittable};
use crate::ray::Ray;
 
#[derive(Default)]
pub struct HittableList {
    objects: Vec<Box<dyn Hittable>>,
}
 
impl HittableList {
    pub fn new() -> HittableList {
        Default::default()
    }
 
    pub fn add(&mut self, object: Box<dyn Hittable>) {
        self.objects.push(object);
    }
}
 
impl Hittable for HittableList {
    fn hit(&self, ray: &Ray, t_min: f64, t_max: f64, rec: &mut HitRecord) -> bool {
        let mut temp_rec = HitRecord::new();
        let mut hit_anything = false;
        let mut closest_so_far = t_max;
 
        for object in &self.objects {
            if object.hit(ray, t_min, closest_so_far, &mut temp_rec) {
                hit_anything = true;
                closest_so_far = temp_rec.t;
                *rec = temp_rec.clone();
            }
        }
 
        hit_anything
    }
}

Common Constants and Utility Functions

We need some math constants that we conveniently define in their own file. For now we only need infinity and pi. We’ll throw future utility functions in the file.

common.rs | The common module

// Constants
 
pub use std::f64::consts::PI;
pub use std::f64::INFINITY;
 
// Utility functions
 
pub fn degrees_to_radians(degrees: f64) -> f64 {
    degrees * PI / 180.0
}

And the new main:

main.rs | The new main with Hittables

mod color;
mod common;
mod hittable;
mod hittable_list;
mod ray;
mod sphere;
mod vec3;
 
use std::io;
 
use color::Color;
use hittable::{HitRecord, Hittable};
use hittable_list::HittableList;
use ray::Ray;
use sphere::Sphere;
use vec3::{Point3, Vec3};
 
fn ray_color(r: &Ray, world: &dyn Hittable) -> Color {
    let mut rec = HitRecord::new();
    if world.hit(r, 0.0, common::INFINITY, &mut rec) {
        return 0.5 * (rec.normal + Color::new(1.0, 1.0, 1.0));
    }
 
    let unit_direction = vec3::unit_vector(r.direction());
    let t = 0.5 * (unit_direction.y() + 1.0);
    (1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
 
fn main() {
    // Image
 
    const ASPECT_RATIO: f64 = 16.0 / 9.0;
    const IMAGE_WIDTH: i32 = 400;
    const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
 
    // World
 
    let mut world = HittableList::new();
    world.add(Box::new(Sphere::new(Point3::new(0.0, 0.0, -1.0), 0.5)));
    world.add(Box::new(Sphere::new(Point3::new(0.0, -100.5, -1.0), 100.0)));
 
    // Camera
 
    let viewport_height = 2.0;
    let viewport_width = ASPECT_RATIO * viewport_height;
    let focal_length = 1.0;
 
    let origin = Point3::new(0.0, 0.0, 0.0);
    let horizontal = Vec3::new(viewport_width, 0.0, 0.0);
    let vertical = Vec3::new(0.0, viewport_height, 0.0);
    let lower_left_corner =
        origin - horizontal / 2.0 - vertical / 2.0 - Vec3::new(0.0, 0.0, focal_length);
 
    // Render
 
    print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
 
    for j in (0..IMAGE_HEIGHT).rev() {
        eprint!("\rScanlines remaining: {} ", j);
        for i in 0..IMAGE_WIDTH {
            let u = i as f64 / (IMAGE_WIDTH - 1) as f64;
            let v = j as f64 / (IMAGE_HEIGHT - 1) as f64;
            let r = Ray::new(
                origin,
                lower_left_corner + u * horizontal + v * vertical - origin,
            );
            let pixel_color = ray_color(&r, &world);
            color::write_color(&mut io::stdout(), pixel_color);
        }
    }
 
    eprint!("\nDone.\n");
}

This yields a picture that is really just a visualization of where the spheres are along with their surface normal. This is often a great way to look at your model for flaws and characteristics.

Resulting render of normals-colored sphere with ground

5. Adding a Sphere 7. Antialiasing