Adding a Sphere

Let’s add a single object to our ray tracer. People often use spheres in ray tracers because calculating whether a ray hits a sphere is pretty straightforward.

Ray-Sphere Intersection

Recall that the equation for a sphere centered at the origin of radius $R$ is $x^2 + y^2 + z^2 = R^2$. Put another way, if a given point $(x,y,z)$ is on the sphere, then $x^2 + y^2 + z^2 = R^2$. If the given point $(x,y,z)$ is inside the sphere, then $x^2 + y^2 + z^2 < R^2$, and if a given point $(x,y,z)$ is outside the sphere, then $x^2 + y^2 + z^2 > R^2$.

It gets uglier if the sphere center is at $(C_x, C_y, C_z)$:

In graphics, you almost always want your formulas to be in terms of vectors so all the x/y/z stuff is under the hood in the Vec3 class. You might note that the vector from center $\mathbf{C} = (C_x,C_y,C_z)$ to point $\mathbf{P} = (x,y,z)$ is $(\mathbf{P} - \mathbf{C})$, and therefore

So the equation of the sphere in vector form is:

We can read this as “any point $\mathbf{P}$ that satisfies this equation is on the sphere”. We want to know if our ray $\mathbf{P}(t) = \mathbf{A} + t\mathbf{b}$ ever hits the sphere anywhere. If it does hit the sphere, there is some $t$ for which $\mathbf{P}(t)$ satisfies the sphere equation. So we are looking for any $t$ where this is true:

or expanding the full form of the ray $\mathbf{P}(t)$:

The rules of vector algebra are all that we would want here. If we expand that equation and move all the terms to the left hand side we get:

The vectors and $r$ in that equation are all constant and known. The unknown is $t$, and the equation is a quadratic, like you probably saw in your high school math class. We can solve for $t$ using the quadratic formula:

Where:

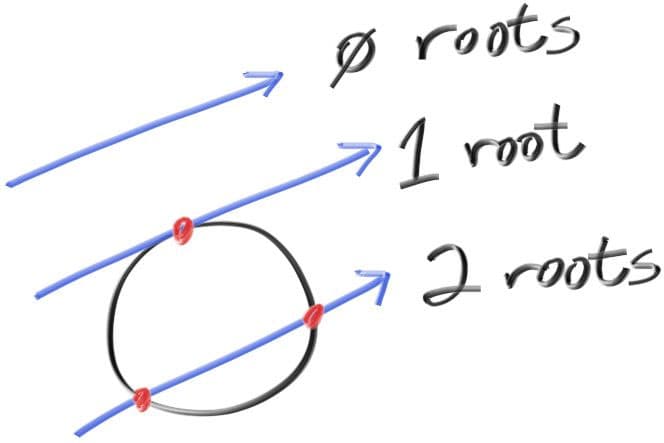
The square root part is called discriminant. It is either positive (meaning two real solutions), zero (meaning one real solution), or negative (meaning no real solutions). In graphics, the algebra almost always relates very directly to the geometry. What we have is:

Creating Our First Ray-traced Image

If we take that math and hard-code it into our program, we can test it by coloring red any pixel that hits a small sphere we place at -1 on the z-axis:

mod color;
mod ray;
mod vec3;
 
use std::io;
 
use color::Color;
use ray::Ray;
use vec3::{Point3, Vec3};
 
fn hit_sphere(center: Point3, radius: f64, r: &Ray) -> bool {
    let oc = r.origin() - center;
    let a = vec3::dot(r.direction(), r.direction());
    let b = 2.0 * vec3::dot(oc, r.direction());
    let c = vec3::dot(oc, oc) - radius * radius;
    let discriminant = b * b - 4.0 * a * c;
    discriminant >= 0.0
}
 
fn ray_color(r: &Ray) -> Color {
    if hit_sphere(Point3::new(0.0, 0.0, -1.0), 0.5, r) {
        return Color::new(1.0, 0.0, 0.0);
    }
 
    let unit_direction = vec3::unit_vector(r.direction());
    let t = 0.5 * (unit_direction.y() + 1.0);
    (1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
 
fn main() {
    // Image
 
    const ASPECT_RATIO: f64 = 16.0 / 9.0;
    const IMAGE_WIDTH: i32 = 400;
    const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
 
    // Camera
 
    let viewport_height = 2.0;
    let viewport_width = ASPECT_RATIO * viewport_height;
    let focal_length = 1.0;
 
    let origin = Point3::new(0.0, 0.0, 0.0);
    let horizontal = Vec3::new(viewport_width, 0.0, 0.0);
    let vertical = Vec3::new(0.0, viewport_height, 0.0);
    let lower_left_corner =
        origin - horizontal / 2.0 - vertical / 2.0 - Vec3::new(0.0, 0.0, focal_length);
 
    // Render
 
    print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
 
    for j in (0..IMAGE_HEIGHT).rev() {
        eprint!("\rScanlines remaining: {} ", j);
        for i in 0..IMAGE_WIDTH {
            let u = i as f64 / (IMAGE_WIDTH - 1) as f64;
            let v = j as f64 / (IMAGE_HEIGHT - 1) as f64;
            let r = Ray::new(
                origin,
                lower_left_corner + u * horizontal + v * vertical - origin,
            );
            let pixel_color = ray_color(&r);
            color::write_color(&mut io::stdout(), pixel_color);
        }
    }
 
    eprint!("\nDone.\n");
}

What we get is this:

Now this lacks all sorts of things — like shading and reflection rays and more than one object — but we are closer to halfway done than we are to our start! One thing to be aware of is that we tested whether the ray hits the sphere at all, but $t < 0$ solutions work fine. If you change your sphere center to $z = +1$ you will get exactly the same picture because you see the things behind you. This is not a feature! We’ll fix those issues next.