Metal
An Abstract Trait for Materials
If we want different objects to have different materials, we have a design decision. We could have a universal material with lots of parameters and different material types just zero out some of those parameters. Or we could have an abstract Material trait that encapsulates behavior. We’ll adopt the latter approach.
For our program the material needs to do two things:
-
Produce a scattered ray (or say it absorbed the incident ray).
-
If scattered, say how much the ray should be attenuated.
This suggests:
material.rs | The Material trait
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
pub trait Material {
fn scatter(
&self,
r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool;
}A Data Structure to Describe Ray-Object Intersections
The HitRecord is to avoid a bunch of arguments so we can stuff whatever info we want in there. You can use arguments instead; it’s a matter of taste.
hittable.rs | HitRecord with added pointer to Material trait object
use std::rc::Rc;
use crate::material::Material;
use crate::ray::Ray;
use crate::vec3::{self, Point3, Vec3};
#[derive(Clone, Default)]
pub struct HitRecord {
pub p: Point3,
pub normal: Vec3,
pub mat: Option<Rc<dyn Material>>,
pub t: f64,
pub front_face: bool,
}
impl HitRecord {
pub fn new() -> HitRecord {
Default::default()
}
pub fn set_face_normal(&mut self, r: &Ray, outward_normal: Vec3) {
self.front_face = vec3::dot(r.direction(), outward_normal) < 0.0;
self.normal = if self.front_face {
outward_normal
} else {
-outward_normal
};
}
}
pub trait Hittable {
fn hit(&self, ray: &Ray, t_min: f64, t_max: f64, rec: &mut HitRecord) -> bool;
}What we have set up here is that Material will tell us how rays interact with the surface. HitRecord is just a way to stuff a bunch of arguments into a struct so we can send them as a group. When a ray hits a surface (a particular sphere for example), the material pointer in the HitRecord will be set to point at the material pointer the sphere was given when it was set up in main() when we start. When the ray_color() routine gets the HitRecord it can call methods of the material pointer to find out what ray, if any, is scattered.
🦀
The Rc smart pointer allow us to share ownership. Here we have to wrap Option around Rc because the corresponding C++ implementation uses std::shared_ptr, which by default initializes the value as nullptr. In Rust, Rc is not nullable. But we can use the Option enum to express the nullability while still achieving memory safety. In the Appendix, we will revisit the code and remove this Option.
To achieve this, we must have a pointer to the material for our Sphere struct to return within HitRecord. See the highlighted lines below:
sphere.rs | Ray-sphere intersection with added Material information
use std::rc::Rc;
use crate::hittable::{HitRecord, Hittable};
use crate::material::Material;
use crate::ray::Ray;
use crate::vec3::{self, Point3};
pub struct Sphere {
center: Point3,
radius: f64,
mat: Rc<dyn Material>,
}
impl Sphere {
pub fn new(cen: Point3, r: f64, m: Rc<dyn Material>) -> Sphere {
Sphere {
center: cen,
radius: r,
mat: m,
}
}
}
impl Hittable for Sphere {
fn hit(&self, r: &Ray, t_min: f64, t_max: f64, rec: &mut HitRecord) -> bool {
let oc = r.origin() - self.center;
let a = r.direction().length_squared();
let half_b = vec3::dot(oc, r.direction());
let c = oc.length_squared() - self.radius * self.radius;
let discriminant = half_b * half_b - a * c;
if discriminant < 0.0 {
return false;
}
let sqrt_d = f64::sqrt(discriminant);
// Find the nearest root that lies in the acceptable range
let mut root = (-half_b - sqrt_d) / a;
if root <= t_min || t_max <= root {
root = (-half_b + sqrt_d) / a;
if root <= t_min || t_max <= root {
return false;
}
}
rec.t = root;
rec.p = r.at(rec.t);
let outward_normal = (rec.p - self.center) / self.radius;
rec.set_face_normal(r, outward_normal);
rec.mat = Some(self.mat.clone());
true
}
}Modeling Light Scatter and Reflectance
For the Lambertian (diffuse) case we already have, it can either scatter always and attenuate by its reflectance , or it can scatter with no attenuation but absorb the fraction of the rays, or it could be a mixture of those strategies. For Lambertian materials we get this simple class:
material.rs | The Lambertian Material struct
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
use crate::vec3;
pub trait Material {
fn scatter(
&self,
r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool;
}
pub struct Lambertian {
albedo: Color,
}
impl Lambertian {
pub fn new(a: Color) -> Lambertian {
Lambertian { albedo: a }
}
}
impl Material for Lambertian {
fn scatter(
&self,
_r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool {
let mut scatter_direction = rec.normal + vec3::random_unit_vector();
*attenuation = self.albedo;
*scattered = Ray::new(rec.p, scatter_direction);
true
}
}Note we could just as well only scatter with some probability and have attenuation be . Your choice.
If you read the code above carefully, you’ll notice a small chance of mischief. If the random unit vector we generate is exactly opposite the normal vector, the two will sum to zero, which will result in a zero scatter direction vector. This leads to bad scenarios later on (infinities and NaNs), so we need to intercept the condition before we pass it on.
In service of this, we’ll create a new vector method — Vec3::near_zero() — that returns true if the vector is very close to zero in all dimensions.
vec3.rs | The vec3::near_zero() method
use std::fmt::{Display, Formatter, Result};
use std::ops::{Add, AddAssign, Div, DivAssign, Mul, MulAssign, Neg, Sub};
use crate::common;
#[derive(Copy, Clone, Default)]
pub struct Vec3 {
e: [f64; 3],
}
impl Vec3 {
pub fn new(x: f64, y: f64, z: f64) -> Vec3 {
Vec3 { e: [x, y, z] }
}
pub fn random() -> Vec3 {
Vec3::new(
common::random_double(),
common::random_double(),
common::random_double(),
)
}
pub fn random_range(min: f64, max: f64) -> Vec3 {
Vec3::new(
common::random_double_range(min, max),
common::random_double_range(min, max),
common::random_double_range(min, max),
)
}
pub fn x(&self) -> f64 {
self.e[0]
}
pub fn y(&self) -> f64 {
self.e[1]
}
pub fn z(&self) -> f64 {
self.e[2]
}
pub fn length(&self) -> f64 {
f64::sqrt(self.length_squared())
}
pub fn length_squared(&self) -> f64 {
self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
}
pub fn near_zero(&self) -> bool {
const EPS: f64 = 1.0e-8;
// Return true if the vector is close to zero in all dimensions
self.e[0].abs() < EPS && self.e[1].abs() < EPS && self.e[2].abs() < EPS
}
}
// Type alias
pub type Point3 = Vec3;
// Output formatting
impl Display for Vec3 {
fn fmt(&self, f: &mut Formatter) -> Result {
write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
}
}
// -Vec3
impl Neg for Vec3 {
type Output = Vec3;
fn neg(self) -> Vec3 {
Vec3::new(-self.x(), -self.y(), -self.z())
}
}
// Vec3 += Vec3
impl AddAssign for Vec3 {
fn add_assign(&mut self, v: Vec3) {
*self = *self + v;
}
}
// Vec3 *= f64
impl MulAssign<f64> for Vec3 {
fn mul_assign(&mut self, t: f64) {
*self = *self * t;
}
}
// Vec3 /= f64
impl DivAssign<f64> for Vec3 {
fn div_assign(&mut self, t: f64) {
*self = *self / t;
}
}
// Vec3 + Vec3
impl Add for Vec3 {
type Output = Vec3;
fn add(self, v: Vec3) -> Vec3 {
Vec3::new(self.x() + v.x(), self.y() + v.y(), self.z() + v.z())
}
}
// Vec3 - Vec3
impl Sub for Vec3 {
type Output = Vec3;
fn sub(self, v: Vec3) -> Vec3 {
Vec3::new(self.x() - v.x(), self.y() - v.y(), self.z() - v.z())
}
}
// Vec3 * Vec3
impl Mul for Vec3 {
type Output = Vec3;
fn mul(self, v: Vec3) -> Vec3 {
Vec3::new(self.x() * v.x(), self.y() * v.y(), self.z() * v.z())
}
}
// f64 * Vec3
impl Mul<Vec3> for f64 {
type Output = Vec3;
fn mul(self, v: Vec3) -> Vec3 {
Vec3::new(self * v.x(), self * v.y(), self * v.z())
}
}
// Vec3 * f64
impl Mul<f64> for Vec3 {
type Output = Vec3;
fn mul(self, t: f64) -> Vec3 {
Vec3::new(self.x() * t, self.y() * t, self.z() * t)
}
}
// Vec3 / f64
impl Div<f64> for Vec3 {
type Output = Vec3;
fn div(self, t: f64) -> Vec3 {
Vec3::new(self.x() / t, self.y() / t, self.z() / t)
}
}
pub fn dot(u: Vec3, v: Vec3) -> f64 {
u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
}
pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
Vec3::new(
u.e[1] * v.e[2] - u.e[2] * v.e[1],
u.e[2] * v.e[0] - u.e[0] * v.e[2],
u.e[0] * v.e[1] - u.e[1] * v.e[0],
)
}
pub fn unit_vector(v: Vec3) -> Vec3 {
v / v.length()
}
pub fn random_in_unit_sphere() -> Vec3 {
loop {
let p = Vec3::random_range(-1.0, 1.0);
if p.length_squared() >= 1.0 {
continue;
}
return p;
}
}
pub fn random_unit_vector() -> Vec3 {
unit_vector(random_in_unit_sphere())
}material.rs | Lambertian scatter, bullet-proof
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
use crate::vec3;
pub trait Material {
fn scatter(
&self,
r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool;
}
pub struct Lambertian {
albedo: Color,
}
impl Lambertian {
pub fn new(a: Color) -> Lambertian {
Lambertian { albedo: a }
}
}
impl Material for Lambertian {
fn scatter(
&self,
_r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool {
let mut scatter_direction = rec.normal + vec3::random_unit_vector();
// Catch degenerate scatter direction
if scatter_direction.near_zero() {
scatter_direction = rec.normal;
}
*attenuation = self.albedo;
*scattered = Ray::new(rec.p, scatter_direction);
true
}
}Mirrored Light Reflection
For smooth metals the ray won’t be randomly scattered. The key math is: how does a ray get reflected from a metal mirror? Vector math is our friend here:
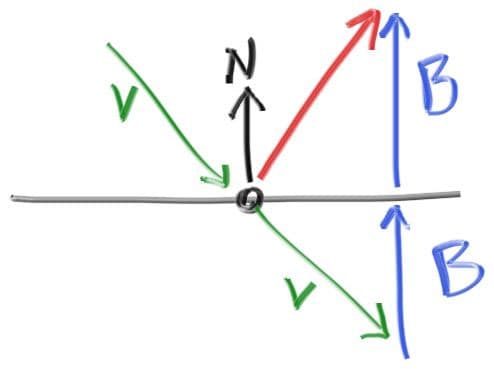
The reflected ray direction in red is just . In our design, is a unit vector, but may not be. The length of should be . Because points in, we will need a minus sign, yielding:
vec3.rs | Vec3 reflection function
use std::fmt::{Display, Formatter, Result};
use std::ops::{Add, AddAssign, Div, DivAssign, Mul, MulAssign, Neg, Sub};
use crate::common;
#[derive(Copy, Clone, Default)]
pub struct Vec3 {
e: [f64; 3],
}
impl Vec3 {
pub fn new(x: f64, y: f64, z: f64) -> Vec3 {
Vec3 { e: [x, y, z] }
}
pub fn random() -> Vec3 {
Vec3::new(
common::random_double(),
common::random_double(),
common::random_double(),
)
}
pub fn random_range(min: f64, max: f64) -> Vec3 {
Vec3::new(
common::random_double_range(min, max),
common::random_double_range(min, max),
common::random_double_range(min, max),
)
}
pub fn x(&self) -> f64 {
self.e[0]
}
pub fn y(&self) -> f64 {
self.e[1]
}
pub fn z(&self) -> f64 {
self.e[2]
}
pub fn length(&self) -> f64 {
f64::sqrt(self.length_squared())
}
pub fn length_squared(&self) -> f64 {
self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
}
pub fn near_zero(&self) -> bool {
const EPS: f64 = 1.0e-8;
// Return true if the vector is close to zero in all dimensions
self.e[0].abs() < EPS && self.e[1].abs() < EPS && self.e[2].abs() < EPS
}
}
// Type alias
pub type Point3 = Vec3;
// Output formatting
impl Display for Vec3 {
fn fmt(&self, f: &mut Formatter) -> Result {
write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
}
}
// -Vec3
impl Neg for Vec3 {
type Output = Vec3;
fn neg(self) -> Vec3 {
Vec3::new(-self.x(), -self.y(), -self.z())
}
}
// Vec3 += Vec3
impl AddAssign for Vec3 {
fn add_assign(&mut self, v: Vec3) {
*self = *self + v;
}
}
// Vec3 *= f64
impl MulAssign<f64> for Vec3 {
fn mul_assign(&mut self, t: f64) {
*self = *self * t;
}
}
// Vec3 /= f64
impl DivAssign<f64> for Vec3 {
fn div_assign(&mut self, t: f64) {
*self = *self / t;
}
}
// Vec3 + Vec3
impl Add for Vec3 {
type Output = Vec3;
fn add(self, v: Vec3) -> Vec3 {
Vec3::new(self.x() + v.x(), self.y() + v.y(), self.z() + v.z())
}
}
// Vec3 - Vec3
impl Sub for Vec3 {
type Output = Vec3;
fn sub(self, v: Vec3) -> Vec3 {
Vec3::new(self.x() - v.x(), self.y() - v.y(), self.z() - v.z())
}
}
// Vec3 * Vec3
impl Mul for Vec3 {
type Output = Vec3;
fn mul(self, v: Vec3) -> Vec3 {
Vec3::new(self.x() * v.x(), self.y() * v.y(), self.z() * v.z())
}
}
// f64 * Vec3
impl Mul<Vec3> for f64 {
type Output = Vec3;
fn mul(self, v: Vec3) -> Vec3 {
Vec3::new(self * v.x(), self * v.y(), self * v.z())
}
}
// Vec3 * f64
impl Mul<f64> for Vec3 {
type Output = Vec3;
fn mul(self, t: f64) -> Vec3 {
Vec3::new(self.x() * t, self.y() * t, self.z() * t)
}
}
// Vec3 / f64
impl Div<f64> for Vec3 {
type Output = Vec3;
fn div(self, t: f64) -> Vec3 {
Vec3::new(self.x() / t, self.y() / t, self.z() / t)
}
}
pub fn dot(u: Vec3, v: Vec3) -> f64 {
u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
}
pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
Vec3::new(
u.e[1] * v.e[2] - u.e[2] * v.e[1],
u.e[2] * v.e[0] - u.e[0] * v.e[2],
u.e[0] * v.e[1] - u.e[1] * v.e[0],
)
}
pub fn unit_vector(v: Vec3) -> Vec3 {
v / v.length()
}
pub fn random_in_unit_sphere() -> Vec3 {
loop {
let p = Vec3::random_range(-1.0, 1.0);
if p.length_squared() >= 1.0 {
continue;
}
return p;
}
}
pub fn random_unit_vector() -> Vec3 {
unit_vector(random_in_unit_sphere())
}
pub fn reflect(v: Vec3, n: Vec3) -> Vec3 {
v - 2.0 * dot(v, n) * n
}The metal material just reflects rays using that formula:
material.rs | Metal Material with reflectance function
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
use crate::vec3;
pub trait Material {
fn scatter(
&self,
r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool;
}
pub struct Lambertian {
albedo: Color,
}
impl Lambertian {
pub fn new(a: Color) -> Lambertian {
Lambertian { albedo: a }
}
}
impl Material for Lambertian {
fn scatter(
&self,
_r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool {
let mut scatter_direction = rec.normal + vec3::random_unit_vector();
// Catch degenerate scatter direction
if scatter_direction.near_zero() {
scatter_direction = rec.normal;
}
*attenuation = self.albedo;
*scattered = Ray::new(rec.p, scatter_direction);
true
}
}
pub struct Metal {
albedo: Color,
}
impl Metal {
pub fn new(a: Color) -> Metal {
Metal { albedo: a }
}
}
impl Material for Metal {
fn scatter(
&self,
r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool {
let reflected = vec3::reflect(vec3::unit_vector(r_in.direction()), rec.normal);
*attenuation = self.albedo;
*scattered = Ray::new(rec.p, reflected);
vec3::dot(scattered.direction(), rec.normal) > 0.0
}
}We need to modify the ray_color() function to use this:
main.rs | Ray color with scattered reflectance
mod camera;
mod color;
mod common;
mod hittable;
mod hittable_list;
mod material;
mod ray;
mod sphere;
mod vec3;
use std::io;
use camera::Camera;
use color::Color;
use hittable::{HitRecord, Hittable};
use hittable_list::HittableList;
use ray::Ray;
use sphere::Sphere;
use vec3::Point3;
fn ray_color(r: &Ray, world: &dyn Hittable, depth: i32) -> Color {
// If we've exceeded the ray bounce limit, no more light is gathered
if depth <= 0 {
return Color::new(0.0, 0.0, 0.0);
}
let mut rec = HitRecord::new();
if world.hit(r, 0.001, common::INFINITY, &mut rec) {
let mut attenuation = Color::default();
let mut scattered = Ray::default();
if rec
.mat
.as_ref()
.unwrap()
.scatter(r, &rec, &mut attenuation, &mut scattered)
{
return attenuation * ray_color(&scattered, world, depth - 1);
}
return Color::new(0.0, 0.0, 0.0);
}
let unit_direction = vec3::unit_vector(r.direction());
let t = 0.5 * (unit_direction.y() + 1.0);
(1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
fn main() {
// Image
const ASPECT_RATIO: f64 = 16.0 / 9.0;
const IMAGE_WIDTH: i32 = 400;
const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
const SAMPLES_PER_PIXEL: i32 = 100;
const MAX_DEPTH: i32 = 50;
// World
let mut world = HittableList::new();
world.add(Box::new(Sphere::new(Point3::new(0.0, 0.0, -1.0), 0.5)));
world.add(Box::new(Sphere::new(Point3::new(0.0, -100.5, -1.0), 100.0)));
// Camera
let cam = Camera::new();
// Render
print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
for j in (0..IMAGE_HEIGHT).rev() {
eprint!("\rScanlines remaining: {} ", j);
for i in 0..IMAGE_WIDTH {
let mut pixel_color = Color::new(0.0, 0.0, 0.0);
for _ in 0..SAMPLES_PER_PIXEL {
let u = (i as f64 + common::random_double()) / (IMAGE_WIDTH - 1) as f64;
let v = (j as f64 + common::random_double()) / (IMAGE_HEIGHT - 1) as f64;
let r = cam.get_ray(u, v);
pixel_color += ray_color(&r, &world, MAX_DEPTH);
}
color::write_color(&mut io::stdout(), pixel_color, SAMPLES_PER_PIXEL);
}
}
eprint!("\nDone.\n");
}🦀
Here, we use as_ref() (opens in a new tab) to create a new Option<&dyn Material> value from the Option<dyn Material> owned by rec.mat. Then we use unwrap() (opens in a new tab) to get the borrowed &dyn Material. Using as_ref() is necessary because unwrap() moves the self value. If we remove the as_ref() call, the compiler will say that rec cannot be used in the scatter() method as a whole because rec.mat has been moved by the unwrap() call.
A Scene with Metal Spheres
Now let’s add some metal spheres to our scene:
main.rs | Scene with metal spheres
mod camera;
mod color;
mod common;
mod hittable;
mod hittable_list;
mod material;
mod ray;
mod sphere;
mod vec3;
use std::io;
use std::rc::Rc;
use camera::Camera;
use color::Color;
use hittable::{HitRecord, Hittable};
use hittable_list::HittableList;
use material::{Lambertian, Metal};
use ray::Ray;
use sphere::Sphere;
use vec3::Point3;
fn ray_color(r: &Ray, world: &dyn Hittable, depth: i32) -> Color {
// If we've exceeded the ray bounce limit, no more light is gathered
if depth <= 0 {
return Color::new(0.0, 0.0, 0.0);
}
let mut rec = HitRecord::new();
if world.hit(r, 0.001, common::INFINITY, &mut rec) {
let mut attenuation = Color::default();
let mut scattered = Ray::default();
if rec
.mat
.as_ref()
.unwrap()
.scatter(r, &rec, &mut attenuation, &mut scattered)
{
return attenuation * ray_color(&scattered, world, depth - 1);
}
return Color::new(0.0, 0.0, 0.0);
}
let unit_direction = vec3::unit_vector(r.direction());
let t = 0.5 * (unit_direction.y() + 1.0);
(1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
fn main() {
// Image
const ASPECT_RATIO: f64 = 16.0 / 9.0;
const IMAGE_WIDTH: i32 = 400;
const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
const SAMPLES_PER_PIXEL: i32 = 100;
const MAX_DEPTH: i32 = 50;
// World
let mut world = HittableList::new();
let material_ground = Rc::new(Lambertian::new(Color::new(0.8, 0.8, 0.0)));
let material_center = Rc::new(Lambertian::new(Color::new(0.7, 0.3, 0.3)));
let material_left = Rc::new(Metal::new(Color::new(0.8, 0.8, 0.8)));
let material_right = Rc::new(Metal::new(Color::new(0.8, 0.6, 0.2)));
world.add(Box::new(Sphere::new(
Point3::new(0.0, -100.5, -1.0),
100.0,
material_ground,
)));
world.add(Box::new(Sphere::new(
Point3::new(0.0, 0.0, -1.0),
0.5,
material_center,
)));
world.add(Box::new(Sphere::new(
Point3::new(-1.0, 0.0, -1.0),
0.5,
material_left,
)));
world.add(Box::new(Sphere::new(
Point3::new(1.0, 0.0, -1.0),
0.5,
material_right,
)));
// Camera
let cam = Camera::new();
// Render
print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
for j in (0..IMAGE_HEIGHT).rev() {
eprint!("\rScanlines remaining: {} ", j);
for i in 0..IMAGE_WIDTH {
let mut pixel_color = Color::new(0.0, 0.0, 0.0);
for _ in 0..SAMPLES_PER_PIXEL {
let u = (i as f64 + common::random_double()) / (IMAGE_WIDTH - 1) as f64;
let v = (j as f64 + common::random_double()) / (IMAGE_HEIGHT - 1) as f64;
let r = cam.get_ray(u, v);
pixel_color += ray_color(&r, &world, MAX_DEPTH);
}
color::write_color(&mut io::stdout(), pixel_color, SAMPLES_PER_PIXEL);
}
}
eprint!("\nDone.\n");
}Which gives:
Fuzzy Reflection
We can also randomize the reflected direction by using a small sphere and choosing a new endpoint for the ray:
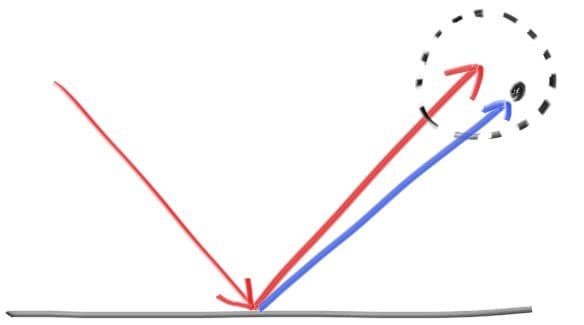
The bigger the sphere, the fuzzier the reflections will be. This suggests adding a fuzziness parameter that is just the radius of the sphere (so zero is no perturbation). The catch is that for big spheres or grazing rays, we may scatter below the surface. We can just have the surface absorb those.
material.rs | Metal Material fuzziness
use crate::color::Color;
use crate::hittable::HitRecord;
use crate::ray::Ray;
use crate::vec3;
pub trait Material {
fn scatter(
&self,
r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool;
}
pub struct Lambertian {
albedo: Color,
}
impl Lambertian {
pub fn new(a: Color) -> Lambertian {
Lambertian { albedo: a }
}
}
impl Material for Lambertian {
fn scatter(
&self,
_r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool {
let mut scatter_direction = rec.normal + vec3::random_unit_vector();
// Catch degenerate scatter direction
if scatter_direction.near_zero() {
scatter_direction = rec.normal;
}
*attenuation = self.albedo;
*scattered = Ray::new(rec.p, scatter_direction);
true
}
}
pub struct Metal {
albedo: Color,
fuzz: f64,
}
impl Metal {
pub fn new(a: Color, f: f64) -> Metal {
Metal {
albedo: a,
fuzz: if f < 1.0 { f } else { 1.0 },
}
}
}
impl Material for Metal {
fn scatter(
&self,
r_in: &Ray,
rec: &HitRecord,
attenuation: &mut Color,
scattered: &mut Ray,
) -> bool {
let reflected = vec3::reflect(vec3::unit_vector(r_in.direction()), rec.normal);
*attenuation = self.albedo;
*scattered = Ray::new(rec.p, reflected + self.fuzz * vec3::random_in_unit_sphere());
vec3::dot(scattered.direction(), rec.normal) > 0.0
}
}We can try that out by adding fuzziness 0.3 and 1.0 to the metals:
main.rs | Metal spheres with fuzziness
mod camera;
mod color;
mod common;
mod hittable;
mod hittable_list;
mod material;
mod ray;
mod sphere;
mod vec3;
use std::io;
use std::rc::Rc;
use camera::Camera;
use color::Color;
use hittable::{HitRecord, Hittable};
use hittable_list::HittableList;
use material::{Lambertian, Metal};
use ray::Ray;
use sphere::Sphere;
use vec3::Point3;
fn ray_color(r: &Ray, world: &dyn Hittable, depth: i32) -> Color {
// If we've exceeded the ray bounce limit, no more light is gathered
if depth <= 0 {
return Color::new(0.0, 0.0, 0.0);
}
let mut rec = HitRecord::new();
if world.hit(r, 0.001, common::INFINITY, &mut rec) {
let mut attenuation = Color::default();
let mut scattered = Ray::default();
if rec
.mat
.as_ref()
.unwrap()
.scatter(r, &rec, &mut attenuation, &mut scattered)
{
return attenuation * ray_color(&scattered, world, depth - 1);
}
return Color::new(0.0, 0.0, 0.0);
}
let unit_direction = vec3::unit_vector(r.direction());
let t = 0.5 * (unit_direction.y() + 1.0);
(1.0 - t) * Color::new(1.0, 1.0, 1.0) + t * Color::new(0.5, 0.7, 1.0)
}
fn main() {
// Image
const ASPECT_RATIO: f64 = 16.0 / 9.0;
const IMAGE_WIDTH: i32 = 400;
const IMAGE_HEIGHT: i32 = (IMAGE_WIDTH as f64 / ASPECT_RATIO) as i32;
const SAMPLES_PER_PIXEL: i32 = 100;
const MAX_DEPTH: i32 = 50;
// World
let mut world = HittableList::new();
let material_ground = Rc::new(Lambertian::new(Color::new(0.8, 0.8, 0.0)));
let material_center = Rc::new(Lambertian::new(Color::new(0.7, 0.3, 0.3)));
let material_left = Rc::new(Metal::new(Color::new(0.8, 0.8, 0.8), 0.3));
let material_right = Rc::new(Metal::new(Color::new(0.8, 0.6, 0.2), 1.0));
world.add(Box::new(Sphere::new(
Point3::new(0.0, -100.5, -1.0),
100.0,
material_ground,
)));
world.add(Box::new(Sphere::new(
Point3::new(0.0, 0.0, -1.0),
0.5,
material_center,
)));
world.add(Box::new(Sphere::new(
Point3::new(-1.0, 0.0, -1.0),
0.5,
material_left,
)));
world.add(Box::new(Sphere::new(
Point3::new(1.0, 0.0, -1.0),
0.5,
material_right,
)));
// Camera
let cam = Camera::new();
// Render
print!("P3\n{} {}\n255\n", IMAGE_WIDTH, IMAGE_HEIGHT);
for j in (0..IMAGE_HEIGHT).rev() {
eprint!("\rScanlines remaining: {} ", j);
for i in 0..IMAGE_WIDTH {
let mut pixel_color = Color::new(0.0, 0.0, 0.0);
for _ in 0..SAMPLES_PER_PIXEL {
let u = (i as f64 + common::random_double()) / (IMAGE_WIDTH - 1) as f64;
let v = (j as f64 + common::random_double()) / (IMAGE_HEIGHT - 1) as f64;
let r = cam.get_ray(u, v);
pixel_color += ray_color(&r, &world, MAX_DEPTH);
}
color::write_color(&mut io::stdout(), pixel_color, SAMPLES_PER_PIXEL);
}
}
eprint!("\nDone.\n");
}